箱线图四分位检测异常值
说明
数据分析教程 正在计划编写中,欢迎大家加微信 gr99123 (备注:数据分析教程) 提供意见、建议、纠错、催更。应大家要求,作者开办数据产品和数据分析培训班,详情 数据产品经理培训 / 数据分析培训。欢迎关注作者出版的书籍:《深入浅出Pandas》 和 《Python之光》。
箱线图四分位检测异常值(Box Plot Diagram to Identify Outliers),箱型图提供了识别异常值的一个标准,即异常值通常被定义为 小于QL-1.5IQR 或大于 QU+1.5IQR 的值。
箱线图识别异常值
离群值是数据序列中的一个极端值,它要么很小,要么很大,因此影响数据序列的整体观测值。异常值也被称为极端值,因为它们位于数据序列的两端。由于其极端值很高或很低,可能影响整体观测,因此应从数据序列中丢弃。
箱线图也称为盒形图,是一种典型的四分位数和四分位数之间的图解法,有助于定义上限和下限,超过上限和下限的任何数据都将被视为异常值。该图表的目的是识别异常值,并在进行进一步观察之前将其从数据系列中剔除,以便研究得出的结论能够给出更准确的结果,而不受任何极端或异常值的影响。
算法
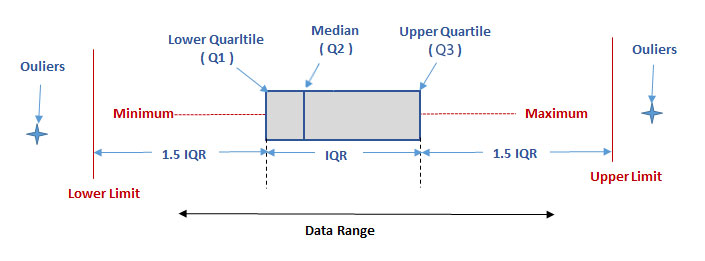
数列的四分位中:
- 四分位距 IQR = Q3 – Q1
- 下界 Lower Limit = Q1 – 1.5 IQR.
- 上界 Upper Limit = Q3 + 1.5 IQR
下界 Lower Limit 和 上界 Upper Limit 之外的数据为异常值。
原理
也就是说,如果数据点低于 Q1–1.5×IQR 或高于 Q3+1.5×IQR,则认为它离中心值太远而不合理。也许你在测量的时候碰了秤,或者你的实验室搭档是个白痴,你不应该让他碰任何设备。谁知道呢?但不管他们的原因是什么,离群值是那些似乎不“适合”的点。
为什么是异常值框宽度的1.5倍?为什么这个特定的值会标记“可接受”和“不可接受”值之间的差异?因为,当 John Tukey 在1977年发明了显示这些值的盒须图时,他选择了 1.5×IQR 作为异常值的去标记线。这很有效,所以我们一直在使用这个值。如果你深入研究统计学,你会发现,对于钟形曲线形状的数据来说,这种合理性度量意味着通常只有大约百分之一的数据是异常值。
代码实现
用 Python 的 Pandas 库:
import pandas as pd
# 检测到异常值置为 nan
def box_plot_outliers(s):
q1, q3 = s.quantile(.25), s.quantile(.75)
iqr = q3 - q1
low, up = q1 - 1.5*iqr, q3 + 1.5*iqr
outlier = s.mask((s<low) | (s>up))
return outlier
参见详细案例:Python 四分位箱线图异常值检测
参考
- https://www.purplemath.com/modules/boxwhisk3.htm
- https://www.whatissixsigma.net/box-plot-diagram-to-identify-outliers/
- https://www.zhihu.com/question/36172806
相关内容
- pandas / Python 四分位箱线图异常值检测 2021-03-03 13:34:56
更新时间:2021-05-25 18:40:27 标签:箱线图 异常值


