平均值 Mean

说明

数据分析教程正在计划编写中，欢迎大家加微信 gairuo123 （备注：数据分析教程）提供意见、建议、纠错、催更。应大家要求，作者开办数据产品和数据分析培训班，详情数据产品经理培训 / 数据分析培训。欢迎关注作者出版的书籍：《深入浅出Pandas》和《Python之光》。

平均值可能是描述集中趋势的最常用方法。要计算平均值，您要做的就是将所有值相加并除以值数。例如，通过将所有分数相加并除以参加考试的学生人数来确定平均分数。

数学中和统计学中有几种平均值，对于数据集，算术平均值（也称为期望值或平均值）是离散数字集的中心值。基本计算方法，是值的总和除以值的数量。

mean 和 average

在英文版的统计学书籍中,经常出现「Average」和「Mean」，但翻译成中文都是「均值」或「平均数」的意思。其实这两个统计术语是有不同的含义的。

average，表示平均，平均数，一般水平，一般标准，所以是种算术平均
mean，也表示平均数，但它既可以是算术平均，也可以是几何平均，或在概率和统计中，随机变量的期望值，即随着样本数的无限增加(如果存在极限)，样本均值趋向集中到的一个极限值

Average	Mean
可以简单地定义为所有数字的总和除以值的总数	可以是集合中最大和最小数字相加并除以 2 的结果
通常以平均值或算术平均值表示	仅是描述样本平均值的一种方法
可以针对假设均一分布的任何离散数计算平均值	它主要用于统计，并且适用于任何分布，例如几何分布，二项式分布，泊松分布等
算术平均值被视为平均值的一种形式	均值有多种类型
通常在日常英语会话中使用平均值	均值是从技术和数学意义上使用
能够为我们提供中位数和众数	不能给出中位数或众数

简单说，average 可以简单地定义为所有数字的总和除以值的总数。 average 通常以平均值或算术平均值表示。 mean 仅是描述样本平均值的一种方法。

公式

$A= \frac {1}{n} \sum \limits_{i=1}^n a_i$

A = 算术平均数（arithmetic mean）
n = 数据数量（number of values）
a_i = 每个数据值（data set values）

示例

有数据 1, 2, 3, 4, 5：

Average = 数据的总和 / 数据的总数
average = (1+2+3+4+5)/5 = 15/5 = 3

以上称为「算术平均数」。

Mean 的一种算法：

Mean = (最大值和最小值之和)/ 2
mean = (1+5)/2 = 6/2 = 3

算术平均数

算术平均数（arithmetic mean）是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。上文中有介绍就不详述了。

数学符号

它的数学符号是 $\bar{x}$

因为 x 上面的横线在英文中读“bar”，中文音译就是“拔”，读作「x拔」。也有读「x 线」、「x 杠」和「x 帽儿」的。

特点

算术平均数是一个良好的集中量数，具有反应灵敏、确定严密、简明易解、计算简单、适合进一步演算和较小受抽样变化的影响等优点。
算术平均数易受极端数据的影响，这是因为平均数反应灵敏，每个数据的或大或小的变化都会影响到最终结果。

加权平均数

加权平均数（weighted average），加权算术平均值与普通算术平均值相似，不同之处在于，某些数据点比其他数据点对最终平均值的贡献均等，而有些数据点对最终平均值的贡献不同。如果所有的权重相同且等于一，那么加权平均数与算术平均数相同。

$W =\frac{\sum_{i=1}^{n} w_{i} X_{i}}{\sum_{i=1}^{n} w_{i}}$

W = 加权平均值 weighted average
n = 要平均的项数 number of terms to be averaged
w_{i} = 应用于x值的权重 weights applied to x values
X_{i} = 要平均的数据值 data values to be averaged

接下来的问题是权重如何计算，可以：

给每个参考计算的值一个权重
权重可以通过此值在数列中的占比计算得出
权重可以通过业务分析人工指定
如果权重用的百分数，一般所有权重相加为 100%

举例如下：

下面是一个同学的某一科的考试成绩：
平时测验 80，期中 90，期末 95
学校规定的科目成绩的计算方式是：
平时测验占 20%；
期中成绩占 30%；
期末成绩占 50%；
这里，每个成绩所占的比重叫做权数或权重。那么，
加权平均值 = 8020% + 9030% + 95*50% = 90.5
算数平均值 = (80 + 90 + 95)/3 = 88.3

上面的例子是已知权重的情况。下面的例子是未知权重的情况：

股票A，1000股，价格10；
股票B，2000股，价格15；
算数平均 = (10 + 15) / 2 = 12.5；
加权平均 = (10 x 1000 + 15 x 2000) / (1000 + 2000) = 13.33
其实，在每一个数的权数相同的情况下，加权平均值就等于算数平均值。

提示：道琼斯工业指数就是算数平均值，标准普尔500指数是权重平均值。

权重

权重是一个相对的概念，是针对某一指标而言。某一指标的权重是指该指标在整体评价中的相对重要程度。权重表示在评价过程中，是被评价对象的不同侧面的重要程度的定量分配，对各评价因子在总体评价中的作用进行区别对待。事实上，没有重点的评价就不算是客观的评价。

几何平均数

几何平均数（geometric mean）为 n 个观察值连乘积的n次方根就是几何平均数。根据资料的条件不同，几何平均数有加权和不加权之分。公式为：

geometric mean

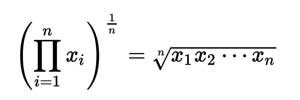
G = 几何平均数（geometric mean）
{n} = 值的数量（number of values）
x_i = 要平均的每个值（values to average）

特点

几何平均数受极端值的影响较算术平均数小。如果变量值有负值,计算出的几何平均数就会成为负数或虚数。

如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时，求各阶段、各环节的一般水平、一般成果，要使用几何平均法计算几何平均数，而不能使用算术平均法计算算术平均数。

用途

主要有：

对比率、指数等进行平均；
计算平均发展速度；
复利下的平均年利率；
连续作业的车间求产品的平均合格率。

其中：样本数据非负，主要用于对数正态分布。

调和平均数

调和平均数（英语：Harmonic mean），是求一组数值的平均数的方法中的一种，一般是在计算平均速率时使用。

调和平均数是将所有数值取倒数并求其算术平均数后，再将此算术平均数取倒数而得，其结果等于数值的个数除以数值倒数的总和。一组正数x1, x2 ... xn的调和平均数H其计算公式为：

$H={\frac {n}{{\frac {1}{x_{1}}} {\frac {1}{x_{2}}} ... {\frac {1}{x_{n}}}}}$

注意，因为0不存在倒数，所以调和平均数不适用于包含0的一组数字。

例如 1，4，4 的调和平均数计算方法
调和平均数 = 3/(1/1 + 1/4 + 1/4) = 2

调和平均数可以用在相同距离但速率不同时，平均速率的计算；如一段路程，前半段时速60公里，后半段时速30公里〔两段距离相等〕，则其平均速率为两者的调和平均数40公里。

在算数平均数中，重要性取决于绝对值大的一方（强），而在调和平均数中，重要性取决于绝对值小的一方（弱）。

平方平均数

平方平均数（Quadratic mean），简称方均根（Root Mean Square，缩写为 RMS），是 2 次方的广义平均数的表达式，也可叫做2次幂平均数。一组数据的平方的平均数的算术平方根。其实就是一组数据的平方的平均数的算术平方根叫做平方平均数。

$Q_n=\sqrt{\frac{x^2_1 x^2_2 ... x^2_n}{n}}=\sqrt{\frac{\sum_{i=1}^{n}x^2_i}{n}} RMS=\sqrt{\frac{1}{n}\sum_i x_i^2}$

RMS / Q_n = 均方根 root mean square
{n} = 量次数 number of measurements
x_i = 每个值 each value

平方平均数起到放大作用，使数据更精确，减少误差。

移动平均数

在股票交易中广泛运用。数学上，移动平均可视为一种卷积。在统计学中，移动平均（英语：moving average）、滚动平均值，又称滑动平均是一种通过创建整个数据集中不同子集的一系列平均数来分析数据点的计算方法。它也是有限脉冲响应滤波器的一种。变化包括: 简单移动平均、指数移动平均、加权移动平均，以及累积移动平均（描述如下）。

给定一个数列和一个固定子集大小，移动平均数的第一个元素是由数列的初始固定子集的平均值得到的。然后通过“向前移位”修改子集，即排除序列的第一个数，并在子集中包含下一个值。

移动平均通常与时间序列数据一起使用，以消除短期波动，突出长期趋势或周期。短期和长期之间的阈值取决于应用，移动平均的参数将相应地设置。例如，它通常用于对财务数据进行技术分析，如股票价格、收益率或交易量。它也用于经济学中研究国内生产总值、就业或其他宏观经济时间序列。数学上，移动平均是卷积的一种类型，因此它可以被看作是用于信号处理的低通滤波器的一个例子。当与非时间序列数据一起使用时，移动平均滤波器的频率分量更高，但与时间没有任何特定的联系，尽管通常暗含某种排序。简单地看，它可以看作是把数据变得更平滑。

可参考窗口计算。

对比

大小关系：调和平均数≤几何平均数≤算术平均数≤平方平均数

代码实现

用 python 实现如下：

from scipy import stats
import numpy as np

r = np.random.default_rng(666)
x = r.integers(1, 100, size=10)
x
# array([89, 76, 26, 55,  7, 54, 34, 61, 48, 34])
# 算术平均数
x.mean()
np.mean(x)
# 48.4

# 加权平均，权重分别从 10 到 1
np.average(x, weights=np.arange(10, 0, -1))
# 53.236363636363635
np.average(x, weights=[1]*len(x)) # 权重全为 1
# 48.4

# 几何平均数
x.prod()**(1.0/len(x))
stats.mstats.gmean(x)
# 40.668301469245236

# 调和平均数
len(x)/np.sum(1.0/x) 
stats.hmean(x)
# 29.54531184602238

# 平方平均数 Root Mean Square
np.sqrt(np.mean(x**2))
# 53.5723809439155

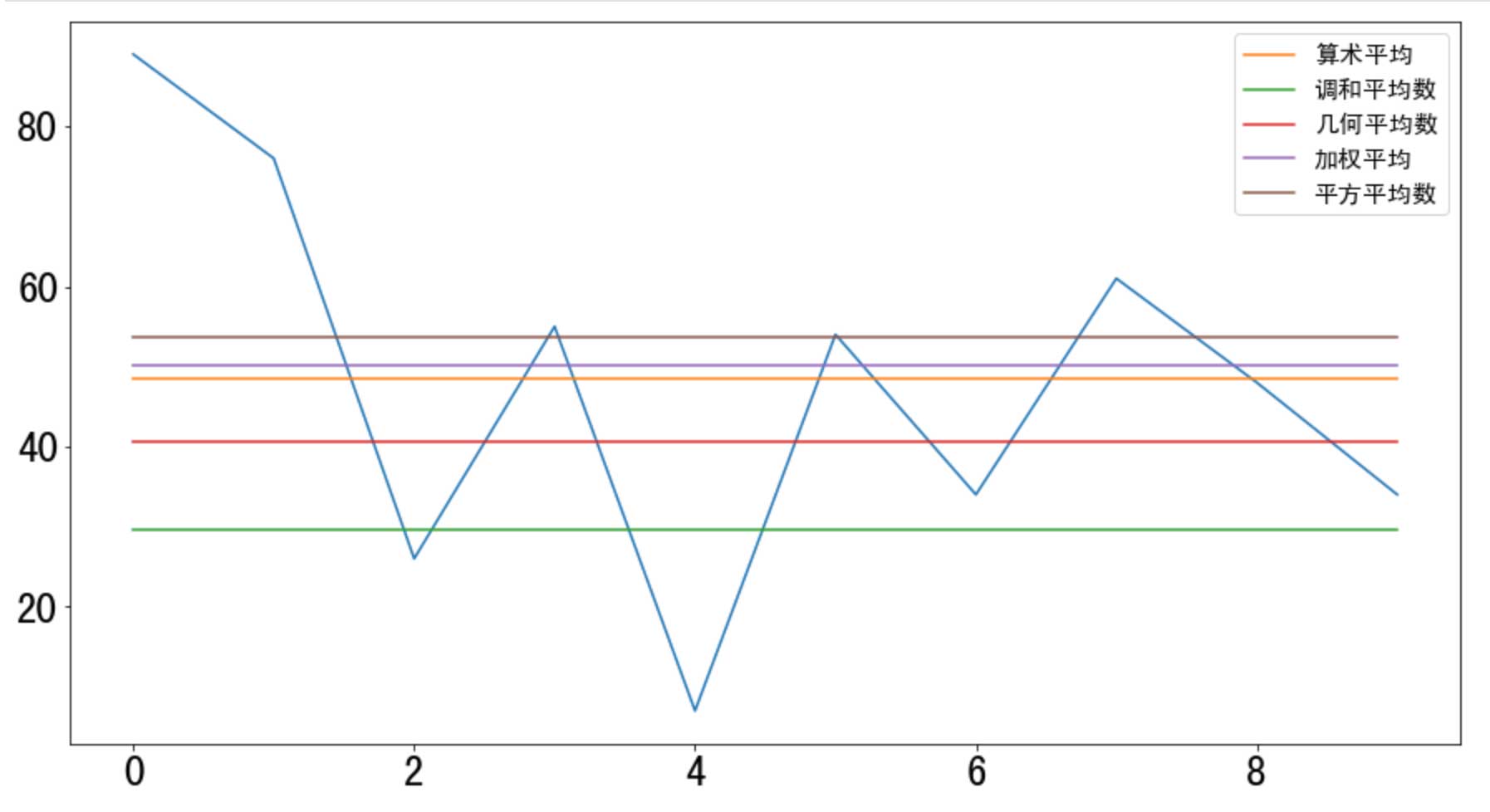
可视化

由于平均值是一个标量（定值），可以将其绘制为一个点或者一条直线方便与数值序列对比：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = (15.0, 8.0) # 固定显示大小
plt.rcParams['font.family'] = ['sans-serif'] # 显示中文问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文问题

r = np.random.default_rng(666)
x = r.integers(1, 100, size=10)
index = np.arange(0, 10) # 建立索引

plt.plot(index, x)
plt.plot(index, [x.mean()]*len(index), label='算术平均')
plt.plot(index, [len(x)/np.sum(1.0/x)]*len(index), label='调和平均数')
plt.plot(index, [x.prod()**(1.0/len(x))]*len(index), label='几何平均数')
plt.plot(index, [np.average(x, weights=np.arange(20, 10, -1))]*len(index), label='加权平均') # 权重分别从 20-10
plt.plot(index, [np.sqrt(np.mean(x**2))]*len(index), label='平方平均数')
plt.legend(fontsize=15)
plt.xticks(fontsize=25)
plt.yticks(fontsize=25)
plt.show()

mean plot

缺失值

一般缺失值不参与计算。

参考

https://byjus.com/maths/difference-between-average-and-mean/

< 描述性统计数据分析教程中位数 Median >

更新时间：2021-01-13 14:17:49 标签：统计数据分析