方差和标准差 Variance / Standard Deviation

方差（Variance）和标准差（Standard Deviation）是统计和概率中重要参数。科学家发现了现实中很多情况，如果只用平均值没有任何参考意义，甚至会误导决策的判断，历史上由罗纳德·费雪首先提出了方差的概念来解决这个问题。

方差开平方根后得到标准差（又称标准偏差、均方差），标准差和原始测量数据具有相同单位，方便分析比较。

方差

方差(variance)示例：

两人的5次测验成绩如下：
A：50，100，100，60，50 Average(A) = 72
B：73，70，75，72，70 Average(B) = 72

以上案例中，平均成绩相同，但A不稳定，对平均值偏大。

方差描述随机变量对于数学期望的偏离程度。它的公式为：

其中：

• S^2 = 样本方差 sample variance
• x_i = 单个观察的值
• \bar{x} = 所有观测值的平均值
• n = 观察次数

将上例中的数据用方差计算得 A 的方差为536，B 的为3.6，很明显，B发挥稳定很多。但是同时出现了一个问题，通过 A B 的方差看不出来与实际测试成绩之间的关系，就是所谓的量纲不一致。因此，就引入了标准差指标。

标准差

标准差（Standard Deviation，简称 SD 或者 STD），就是对应数据方差开平方，用来衡量一组数据的变异性或分散性，单位与该组数据的单位相同。

公式计算

公式为：

上例中 A 和 B 的标准差分别为 23.15 和 1.9，可以将标准差的值解释为他们的成绩在自己的平均成绩上下 23.15 和 1.9 之间变化，这样标准差的单位也是分数，与原数据的单位一致，便于理解。

常见标准差的计算步骤如下：

1. 计算每个值与样本均值之差的平方
2. 将这些值加起来
3. 将总和除以 N-1（此时称为方差），见 ddof 介绍
4. 取平方根求得标准差

δ自由度 ddof

δ自由度（Delta Degrees of Freedom），方差和标准差计算中使用的除数是 N-ddof，其中 N 表示元素数，ddof 就是 δ 自由度。δ自由度也就是第三步中 N 减去的值，在很多复杂的数据分析中，δ 自由度为 1，在常规的计算中一般为 0。Numpy 中默认为 0，Pandas 中默认为 1。

在第三步中，即为什么是除以 N-1 而不是 N？简单说一般样本方差会小于总体方差，所以为了弥补，将 n-1 分子减小，结果大一些。

因为我们想通过样本来推断整体，得出一般性的结论，也就是说我们想知道的是总体的标准差，除以 N-1 算出来的是对总体标准差的最佳估测。在步骤 1 中，计算每个值与平均值之间的差，这里的平均值是样本的平均值，总体的平均值是不知道的，样本的均值与真实的总体均值是有差异的；在第 2 步中算出的值要比使用真实的总体均值要小（不可能大），所以除以 N-1 而不是除以 N。

当然，如果只是量化一组特定数据的变化，并不打算进行推断以得出更广泛的结论，这个时候就除以 N，得出的标准差就是这组特定数据的标准差。比如，在量化考试成绩之间的差异时，全年级全部人的考试成绩都用来分析。

还可以这么理解：因为均值已经用了 n 个数的平均来做估计，在求方差时，只有(n-1)个数和均值信息是不相关的。而你的第ｎ个数已经可以由前(n-1)个数和均值来唯一确定，实际上没有信息量所以在计算方差时，只除以(n-1)。

总之，估计的角度（求期望值）而言用 N-1 是最准确的。一般地 ddof=1 时叫 样本方差（sample variance）或者 样本标准差（Sample Standard Deviation），对应地 ddof=0 叫总体方差，样本方差也可以叫无偏方差（unbiased variance），它们是从概率论与统计学不同的角度出发解决实际问题的。

表示方法

有两种表示方法：

• 平均值±标准差，并且声明后面这个值就是标准差
• 单独表示，是一个单一值

第一种可以知道基数，标准差就是在这个基数上上下浮动。

应用

标准差可以当作不确定性的一种测量。在物理科学中，做重复性测量时，测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值，测量值的标准差占有决定性重要角色。如果测量平均值与预测值相差太远(同时与标准差数值做比较)，则认为测量值与预测值互相矛盾。这很容易理解，因为如果测量值都落在一定数值范围之外，可以合理推论预测值是否正确。

深入理解：从方差到标准差

我们先看这样一个数列：

2，8，9，3，2，7，1，6

我们首先在简单的散点图中绘制这些数字：

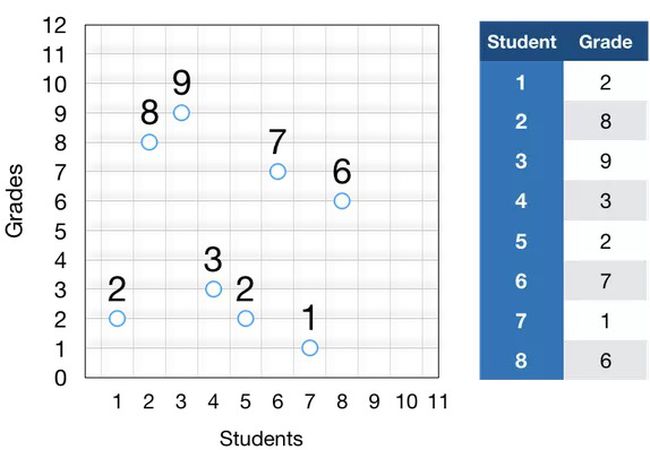
计算差异的第一步是找出这些数字的中心，即平均值，等于 4.75，可以绘制一条线来表示平均分数：

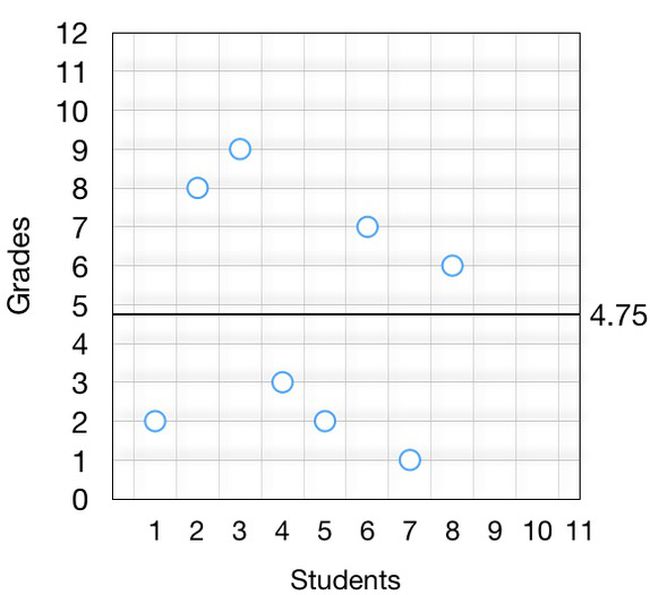
接下来我们要计算每个点和平均值之间的距离，并对得到的数值求平方。记住，我们的目标是计算数字之间的差异，以及数字与平均值之间的差异。我们可以用数学或视图的方式完成该操作：

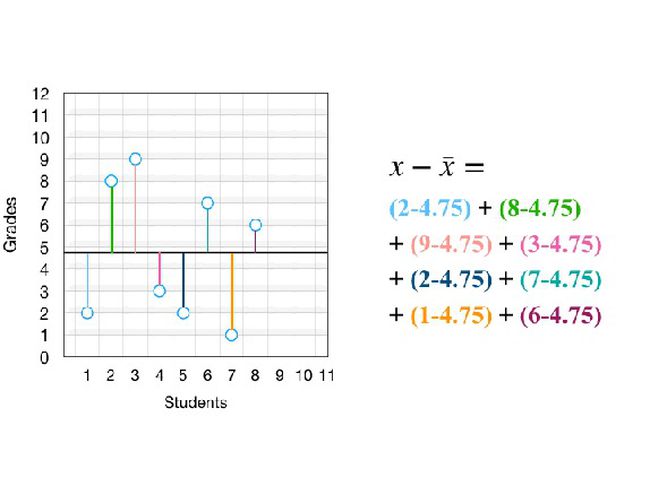
从上图中我们可以看到，「求平方」只不过是画了一个方框而已。这里有两点需要注意：我们无法计算所有差异的总和。因为一些差异是正值，一些是负值，求和会使正负抵消得到 0。为此，我们对差异取平方（稍后我会解释为什么取平方而不是其他运算，如取绝对值）。

现在，我们来计算差异平方的总和（即平方和）：

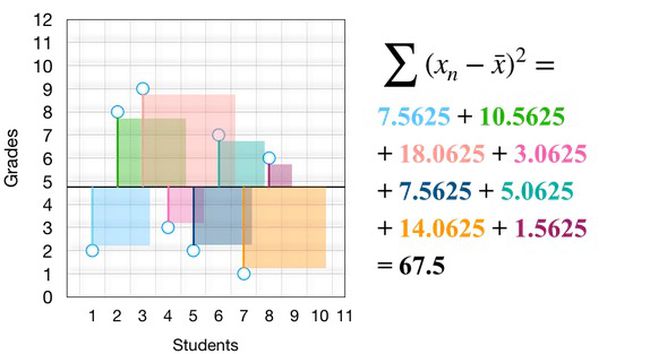
通过计算平方和，我们高效计算出这些分数的总变异（即差异）。理解变异（variability）与差异（difference）之间的关系是理解多个统计估计和推断检验的关键。上图中平方和 67.5 表示，如果我们将所有方框堆在一个巨大的正方形中，则大正方形的面积等于 67.5 points^2，points 指分数的单位。任意测量集的总变异都是正方形的面积。

方差

现在我们得到了总变异（即大正方形的面积），但我们真正想要的是平均变异（mean variability）。要想求得平均变异，我们只需要用总面积除以方框的数量：

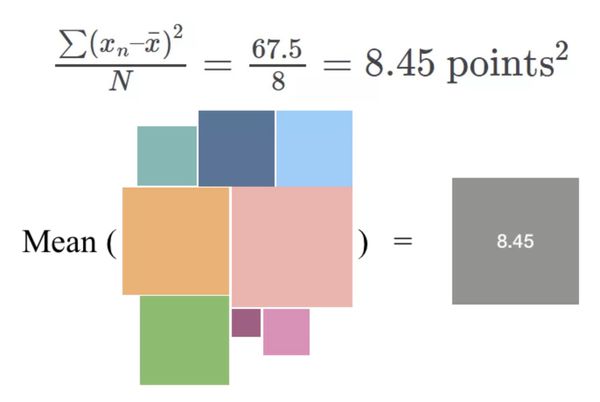
出于实用目的考虑，你或许想除以 N−1，而不是 N，这样你就可以尝试基于一个样本而不是总体来估计平均变异。但是，这里假设我们已经具备总体（total population）。重点在于，你想计算所有小方框的均方值。这就是「方差」，即平均变异，或者差异平方的平均值（mean squared difference）。

标准差

我们为什么不用方差来表示分数的差异呢？唯一的问题是，我们无法对比方差和原始分数，因为方差是「平方」值，即它是面积而非长度。其单位是 points^2，与原始分数的单位 points 不同。那么如何甩掉平方呢？开平方根啊！

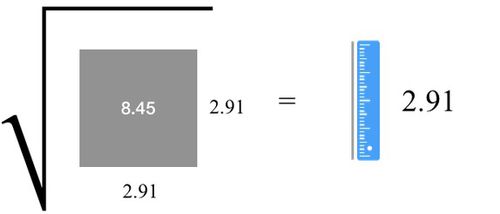
最后，我们终于得到了标准差：变异的平方根，即 2.91points。

这就是标准差的核心理念。本文对标准差概念的基础直观解释可以帮助大家更容易地理解，为什么在处理 z 分数（z-score）、正态分布、标准误差和方差分析时要使用标准差的单位。

此外，如果你用标准差公式中的拟合线 Y 替代平均值，则你在处理的是基础回归项，如均方误差（不开根号的话）、均方根误差（开根号，但是和拟合线相关）。相关和回归公式均可使用不同量的平方和（或总变异区域）来写。分割平方和是理解机器学习中的泛化线性模型和偏差-方差权衡的关键概念。

注：本节选自 https://mp.weixin.qq.com/s/8ukPFsG9mVbrJtPkKvfSTw

代码实现

Python

注：关于 δ自由度（Delta Degrees of Freedom）Numpy 中默认为 0，Pandas 中默认为 1。Pandas 如果按 numpy.std 的标准计算，则需要使用 ddof=0（而不是默认的 ddof=1）

import pandas as pd
import numpy as np

a = [50,100,100,60,50]
ser = pd.Series(a)
arr = np.array(a)

# 方差
ser.var(ddof=0)
np.var(arr)
# 536.0

# 标准差
ser.std(ddof=0)
np.std(arr)
# 23.15167380558045

pandas 和 numpy 计算方差和标准差结果不同的问题：

在计算标准偏差时，重要的是使用较小的总体样本估计整个总体的标准偏差，还是计算整个总体的标准偏差。

如果是较大总体中的较小样本，则需要所谓的样本标准差。事实证明，当你用平均值的平方差之和除以观测值的个数时，你得到的是一个有偏估计量。我们通过除以比观察次数少一的方法来纠正这个错误。我们用参数ddof=1表示样本标准差，或ddof=0表示总体标准差来控制。

事实是，如果你的样本量很大，这并不重要，但你会看到细微的差别。

R

todo

Excel

可使用公式=STDEV.P(C4:C8)来计算标准差，其中 C4:C8 是数据列的区域。excel 中函数 STDEV() 是基于 N-1，函数 STDEVP() 是基于 N 的。

可视化

方差和标准差经常用下列图形表示数据的分布情况：

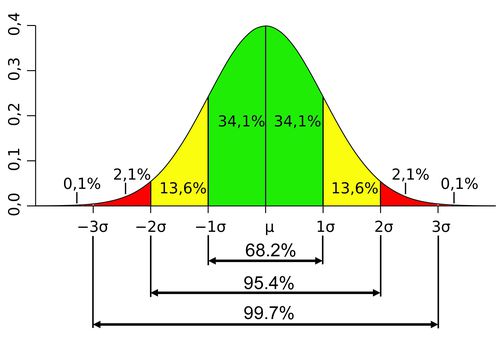
参考

• https://www.zhihu.com/question/20099757/answer/658048814
• https://mp.weixin.qq.com/s/7M2FntTBdJDT-1JC5SqV6w
• https://zhuanlan.zhihu.com/p/157799814
• https://mp.weixin.qq.com/s/8ukPFsG9mVbrJtPkKvfSTw