数据缺失值及处理
说明
数据分析教程 正在计划编写中,欢迎大家加微信 gr99123 (备注:数据分析教程) 提供意见、建议、纠错、催更。应大家要求,作者开办数据产品和数据分析培训班,详情 数据产品经理培训 / 数据分析培训。欢迎关注作者出版的书籍:《深入浅出Pandas》 和 《Python之光》。
野生的数据经常出现缺失值,这个很好理解,我们填写表格也经常心浮气躁,有一些内容可能就漏填了,譬如说在性别一栏留下了空白,这就是缺失值。
相关介绍
在统计调查的过程中,由于受访者对问题的遗漏、拒绝,或是调查员与调查问卷本身存在的一些疏忽,使得记录经常会出现 缺失数据 (Missing Data) 的问题。但是,几乎所有标准统计方法都假设每个个案具有可用于分析的所有变量信息,因此缺失数据就成为进行统计研究或问卷调查的工作人员所必须解决的一个问题。
Paul D. Allison在其2011年出版的Missing Data一书中,提到了许多解决缺失数据问题的方案,而它们各有利弊。
产生原因
缺失值产生的原因有以下几类:
随机缺失 Missing at Random (MAR): 随机缺失是指数据点的缺失倾向与缺失的数据无关,而与某些观测数据有关
完全随机缺失 Missing Completely at Random (MCAR): 某个值丢失的事实与其假设值和其他变量的值无关。
非随机缺失 Missing not at Random (MNAR): 两个可能的原因是缺失值取决于假设值(例如,高薪人群通常不想在调查中透露自己的收入),或者缺失值取决于其他变量的值(例如,假设女性通常不想透露自己的年龄!此处年龄变量中缺少的值受性别变量影响)
在前两种情况下,根据缺失值的出现情况删除缺失值的数据是安全的,而在第三种情况下删除缺失值的观测值可能会在模型中产生偏差。所以我们在移除观测值之前必须非常小心。请注意,插补不一定能给出更好的结果。
处理方式
对于缺失值的处理总体有有两种方法:
- 插补 Imputation
- 删除 Removing Data
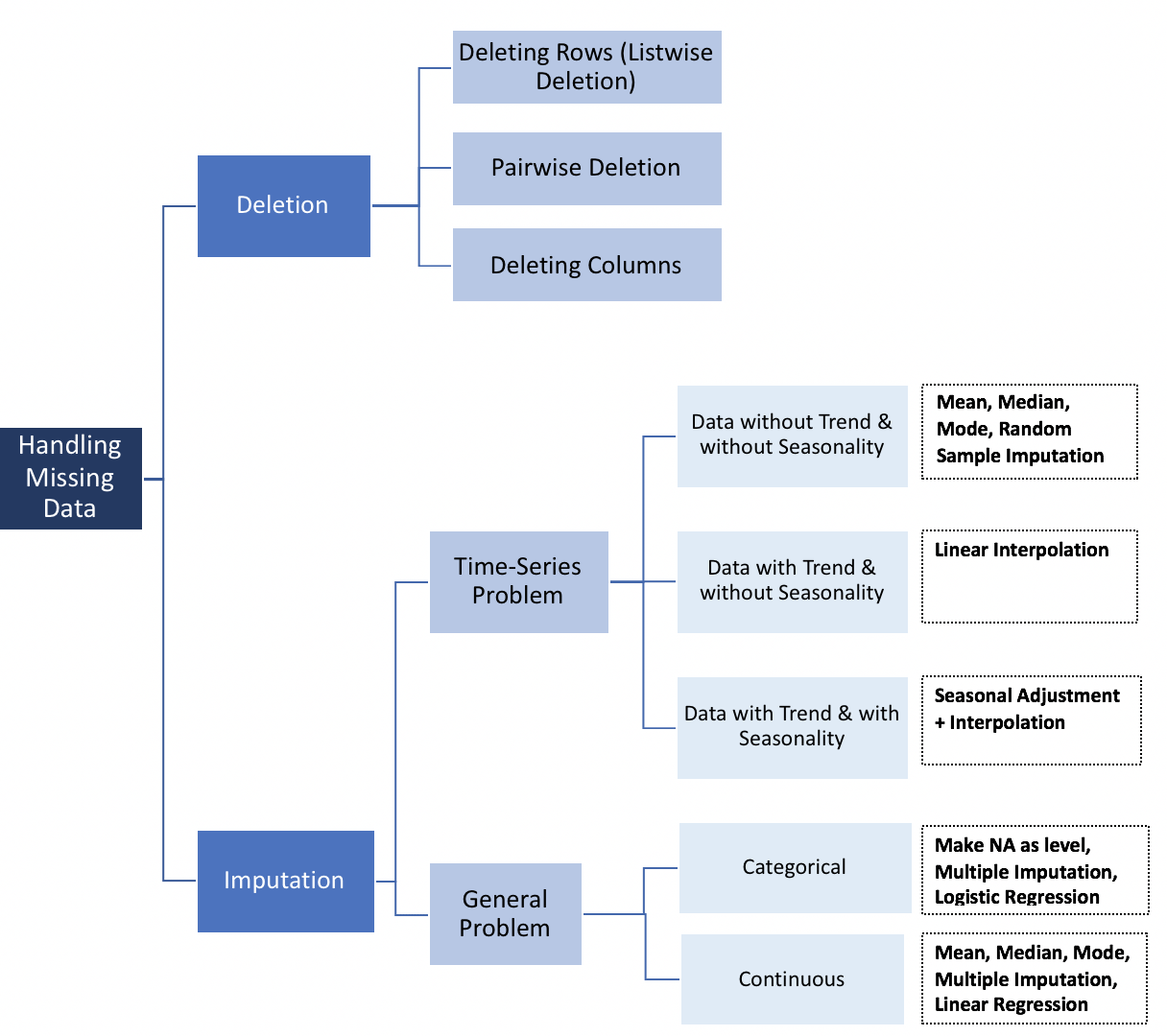
解决缺失数据问题的方法主要有:成列删除、成对删除、虚拟变量调整、插补、多重插补和最大似然。
成列删除
成列删除的思想是:在分析中当某个案的任何变量有缺失数据时,便简单地将该个案从分析中排除。也称为个案删除。
成列删除方法的优点有:
- 可用于任何类型的统计分析。
- 不需要特别的运算方法。
- 如果数据是MCAR,则减少的样本将会是原样本的一个随机次样本。
- 如果任何因变量缺失数据的概率不取决于自变量的值,则使用成列删除的回归估计值将会是无偏误的。
成列删除方法的缺点有:
- 标准误通常较大。
- 如果数据不是MCAR而只是MAR,那么成列删除可能会产生有偏误的估计值。
成对删除
成对删除的原理是:通过所有可得的个案来计算这些描述统计的每一个。成对删除又称可得个案分析。
成对删除方法的优点是:如果数据为MCAR,成对删除就产生一致的参数估计值(在大样本中接近无偏误),且有比成列删除更少的抽样变异(较小的真实标准误),而当变量间相关性普遍较低时,成对删除会产生更有效的估计值。
成对删除方法的缺点有:
- 如果数据是MAR但不是随机被观察到的,估计值可能会严重偏误。
- 由统计软件所产生的标准误和检验统计量估计时偏误的。
- 在小样本中,建构的协方差或相关矩阵可能不是“正定的”。
虚拟变量调整
虚拟变量调整或缺失指标方法:假设某变量X有一些缺失数据,X为回归分析中数个自变量的其中一个,那么可以建立一个虚拟变量D,如果X存在数据缺失则D=1,否则D=0。同时建立一个变量X',使得当不存在数据缺失时X'=X,否则X'等于一个任意常数c。回归因变量Y于X'、D及其他在预设模型中的所有变量。
虚拟变量调整方法的优点是:它使用了所有可用的关于缺失数据的信息。
虚拟变量调整方法的缺点是:它通常会产生有偏误的系数估计值。
插补
插补方法的基本原理是:以某些合理的猜测插补或替代缺失值,然后再接着按没有缺失数据的情况进行分析。但是,按照完整数据的情况分析插补数据会低估标准误、高估检验统计量。
多重插补
多重插补法(MI)具有与最大似然法相同的最适特性,但却排除了某些局限性。特别是当数据为MAR时,正确使用多重插补会产生一致的、渐近有效且渐近正态的估计值。多重插补的另一个优势是,它几乎可以被任何一种数据或模型所使用,且分析可以利用未修改的、传统的软件执行。不过,多重插补也有缺点,它的执行可能很麻烦也很容易出错,最严重的是每次使用多重插补时,都会产生不同的估计值。
最大似然
最大似然是一个有效且实用的处理随机缺失数据的方法,且对于大样本来说是最合适的,但它有一个限制条件:它需要包含所有缺失变量的联合概率的模型。因此比较适合于线性模型和对数线性模型。
- 当缺失数据是MAR时,可以简单地通过加总所有缺失数据可能值的一般似然来获得似然,原来的问题就变成了寻找尽可能使这个似然值最大化的参数值。
- 当缺失数据服从某一单调形态时,可以将似然因子化运用到用传统软件估计的条件式及边际分布中,但是这一方法不容易得到好的标准误及检验统计量的估计值。
- 一般缺失数据模式可用“期望最大化(EM)”的算法来处理,其优点有:容易使用且在很多商业的或免费的软件中都可以执行,缺点为:由线性模型化所报告的软件标准误和检验统计量并不正确,且对于过度识别模型,估计值不是全然有效的。
参考
- wiki
- https://mp.weixin.qq.com/s/HUcmgQVNh30sgUJEGWF1fw
- https://towardsdatascience.com/how-to-handle-missing-data-8646b18db0d4
更新时间:2021-03-14 15:57:48 标签:缺失值 数据


