分位数 Quantile
说明
数据分析教程 正在计划编写中,欢迎大家加微信 gr99123 (备注:数据分析教程) 提供意见、建议、纠错、催更。应大家要求,作者开办数据产品和数据分析培训班,详情 数据产品经理培训 / 数据分析培训。欢迎关注作者出版的书籍:《深入浅出Pandas》 和 《Python之光》。
分位数(英語:Quantile),亦称分位点,是指用分割点(cut point)将一个随机变量的概率分布范围分为几个具有相同概率的连续区间。统计学中,把所有数值由小到大排列并分成四等份,处于三个分割点位置的得分就是四分位数。
定义
在统计和概率中,分位数是将概率分布的范围划分为具有相等概率的连续区间或以相同方式将样本中的观察值划分的切点。 分位数比数据分组应用相对少。
分位数指的就是连续分布函数中的一个点,这个点对应概率 p。若概率0<p<1,随机变量X或它的概率分布的分位数 Za,是指满足条件 p(X≤Za)=α 的实数 。
分位数是计算值,而不是数据中的观测值。通常,需要在两个观测值之间插值才能正确计算出 n 分位数。
四分位
常见的为四分位。四分位数是将数据样本分成四个相等部分的值。利用四分位数,可以快速评估数据集的散布和中心趋势 – 这是了解数据的重要前期步骤。
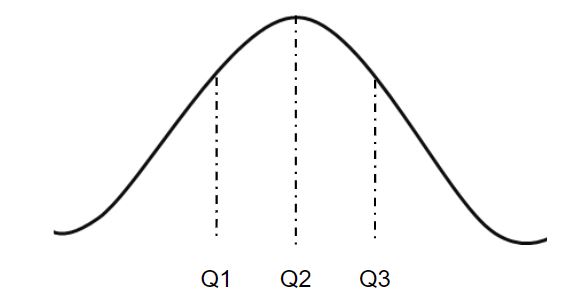
| 四分位数 | 说明 |
|---|---|
| 第一个四分位数 (Q1) | 25% 的数据小于等于此值。 |
| 第二个四分位数 (Q2) | 中位数。50% 的数据小于等于此值。 |
| 第三个四分位数 (Q3) | 75% 的数据小于等于此值。 |
| 四分位间距(IQR) | 第一个四分位数与第三个四分位数之间的距离 (Q3-Q1);因此,它跨越数据中间部分(即 50%)。 |
例如:
例如,对于以下数据:7、9、16、36、39、45、45、46、48、51
Q1 = 14.25
Q2(中位数)= 42
Q3 = 46.50
四分位间距 = 14.25 - 46.50,或 32.25
再例如:
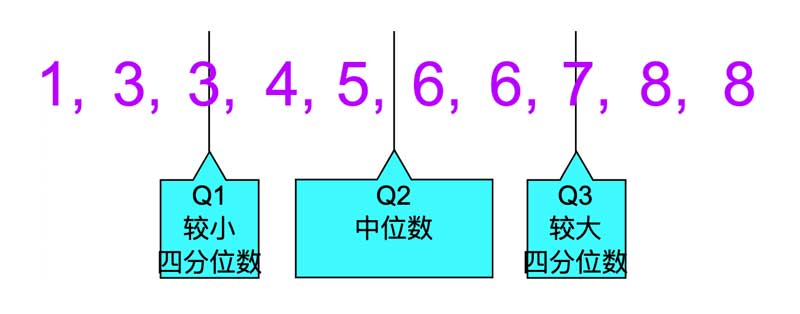
1、3、3、4、5、6、6、7、8、8
数值已经是顺序排列了。把它分成四个四分之一的部分:
在这个例子里,第二个四分位数是在 5 和 6 的正中间:
Q2 = (5+6)/2 = 5.5
结果是:
四分位数 1 (Q1) = 3
四分位数 2 (Q2) = 5.5
四分位数 3 (Q3) = 7
将一个年度时间序列切分为四个分位,每个为一个季度。
四分位距(interquartile range, IQR)。是描述统计学中的一种方法,以确定第三四分位数和第一四分位数的分别(即 Q1 和 Q3 的差距)。与方差、标准差一样,表示统计资料中各变量分散情形,但四分差更多为一种稳健统计(robust statistic)。
百分位
如果有某个百分比的数据低于一个值,这个值便叫百分位数。
例子: 你是班上 20个学生里身高第四的学生
80% 的学生比你矮:你身高是第 80个百分位数(百分等级是 80%)。
如果你的身高是 1.85m,"1.85m" 是班上身高的 80% 百分位数。
todo
分位差
todo
插值方法
则按上面公式计算出来的四分位数的位次就可能带有小数,这时可根据插值法来计算上下四分位数。再按公式计算出四分位差。
todo
代码实现
Python 代码如下:
import pandas as pd
import numpy as np
x = np.array([1,3,5,6,7,9])
# 四分位值
np.quantile(x, 0.25) # 3.5
# 默认二分位
pd.Series(x).quantile() # 5.5
# 插值方法用 higher,默认 linear
pd.Series(x).quantile([1/4, 2/4, 3/4], interpolation='higher')
'''
0.25 5
0.50 6
0.75 7
dtype: int64
'''
# 指定位置
pd.Series(x).quantile([0,0.25,0.5,0.75,1])
'''
0.00 1.00
0.25 3.50
0.50 5.50
0.75 6.75
1.00 9.00
dtype: float64
'''
# pandas 描述统计默认四分位
pd.DataFrame(x).describe()
'''
0
count 6.000000
mean 5.166667
std 2.857738
min 1.000000
25% 3.500000
50% 5.500000
75% 6.750000
max 9.000000
'''
# pandas 指定三分位
pd.DataFrame(x).describe(percentiles=[1/3, 2/3])
'''
0
count 6.000000
mean 5.166667
std 2.857738
min 1.000000
33.3% 4.333333
50% 5.500000
66.7% 6.333333
max 9.000000
'''
缺失值
一般缺失值不参与计算。
意义
- 表示了在这个样本集中从小至大排列之后小于某值的样本子集占总样本集的比例
- 可以识别检测异常值
todo
todo
参考
- https://www.shuxuele.com/data/percentiles.html
更新时间:2021-03-02 18:26:09 标签:统计 数据分析